Geometry pack: What can we learn from star patterns?
Use this pack to explore the geometry of stars with students in KS2.
The six activities in this geometry pack have been developed to explore with students the fascinating geometry of star shapes. They can be used to support learning about shape and number sequences in maths (challenges and short investigations related to shape and number are included throughout), to enrich an exploration of star designs in art or to teach geometry as a standalone activity. These activities are particularly well suited to teaching and learning in the run-up to the festive period, and could be used to support learning about the role of the star in the Christmas story, for example.
For each activity, step-by-step text instructions are provided as a guide for teachers, with accompanying diagrams and lists of the resources students will need to complete each activity. There are also photocopiable templates that teachers can use to provide additional support for those students who need it.
If you have already registered for a free account with us, you will be able to access the pack at any time from the ‘My Account’ section of the website.
To help students get the most out of these activities, we recommend the use of Jakar compasses, which can be purchased at a discounted rate on our website.
What’s in the pack?
The following six activities are available in this pack:
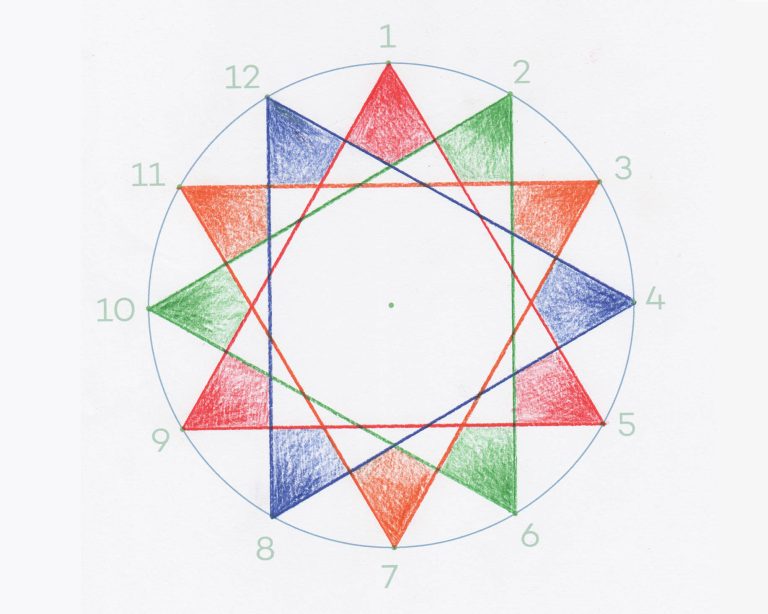
Activity 1 What stars can we make with triangles?
In this activity, students use a template to draw a series of triangles, all of which have their vertices located on the circumference of a circle. These triangles build up to create a 12-pointed star (dodecagram).
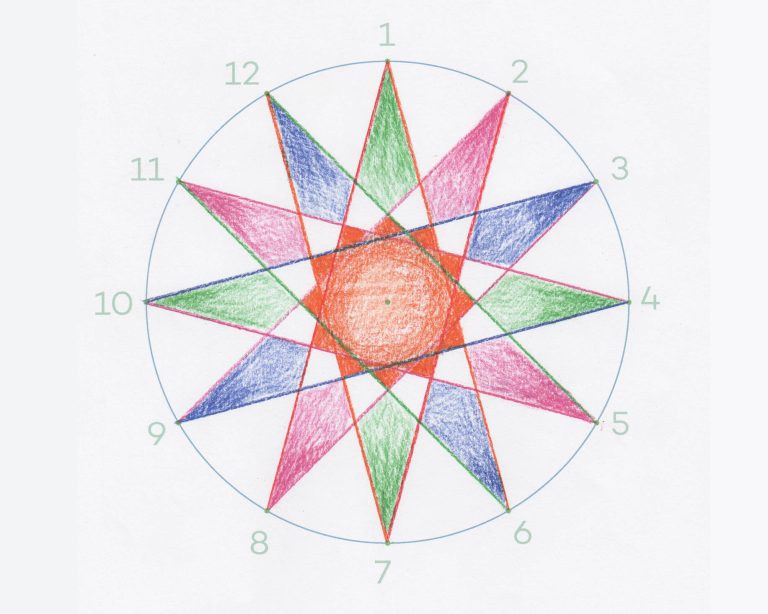
Activity 2 What stars can we make with other shapes?
There are three tasks that make up this activity. In the first task, students use a template to draw a series of squares, all of which have their vertices located on the circumference of a circle. These squares build up to create a 12-pointed star – this is called a ‘dodecagram’. In the second task, they go on to create a dodecagram using hexagons, while in the third task, they explore how pairs of parallel lines can also be used to draw a 12-pointed star.
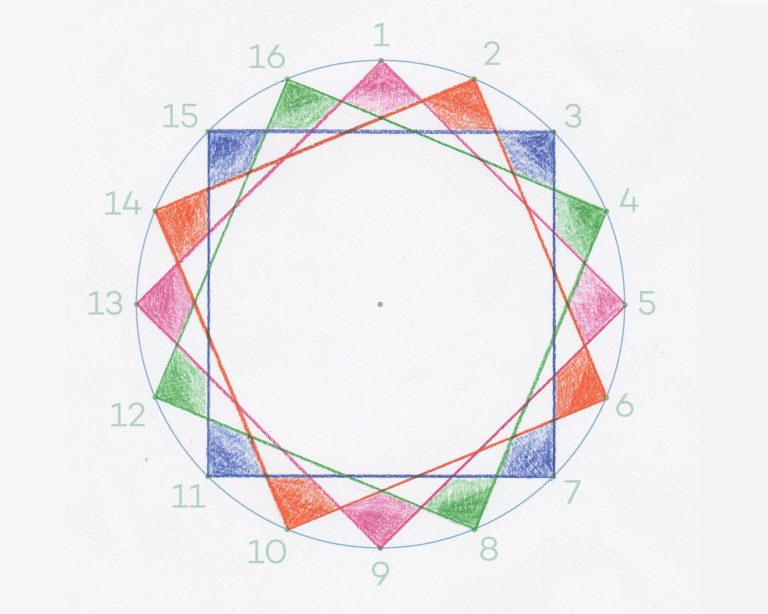
Activity 3 What stars can we make that have 16 points?
This activity is made up of two tasks. In the first, students use a template to draw a series of squares, all of which have their vertices located on the circumference of a circle. These squares build up to create a 16-pointed star. Students go on to explore, in the second task, how pairs of parallel lines can be used to draw an eight-pointed star.
Activity 4 What kind of star can we draw in a square?
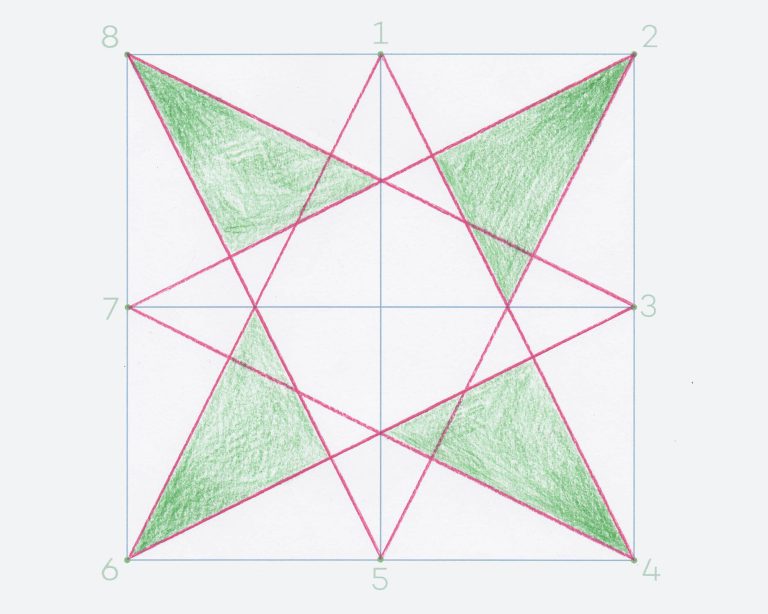
In the first of the two tasks that make up this activity, students draw an eight-pointed, unicursal star using the vertices and the mid-points of each side of a square. A unicursal star is a special kind of star that you can draw without lifting your pencil from the paper and without retracing any lines. In the second tasks, they are challenged to find as many right-angled triangles as they can within the unicursal star they previously drew.
Activity 5 What patterns can we make with 5-pointed stars?
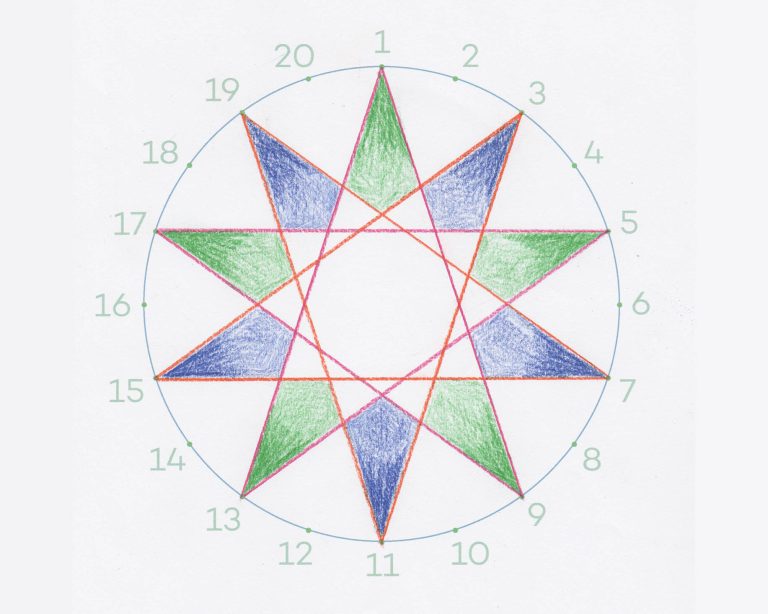
In this activity, students use a template to draw a series of pentagrams, all of which have their vertices located on the circumference of a circle. When four pentagrams are drawn on one template, a 20-pointed star is created.
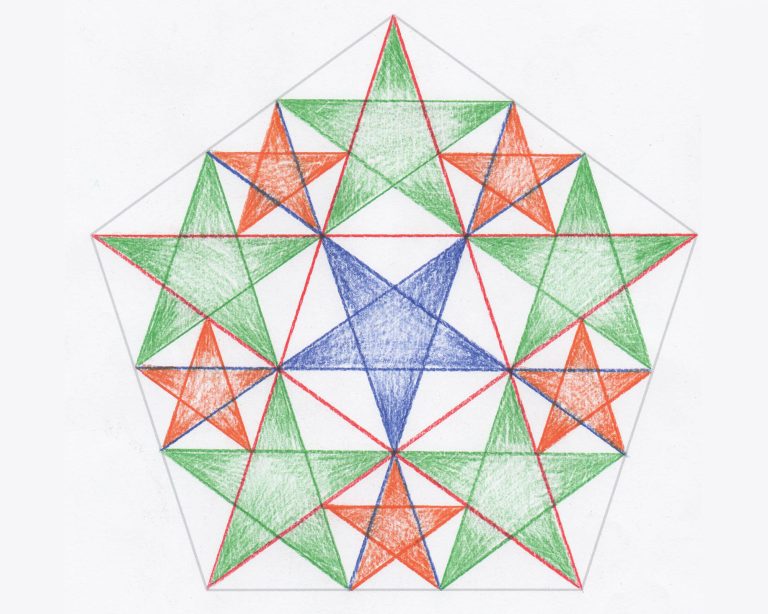
Activity 6 How can I create a design using pentagrams?
In this activity, students use a template to draw a pentagram (the shape we might call a regular, five-pointed star) inside a pentagon. They then continue adding lines within the pentagon to create other pentagrams. This activity encourages a deeper understanding of the pentagon and pentagram and allows students to recognise the relationships between different shapes.
